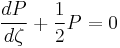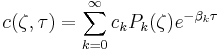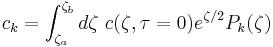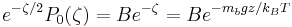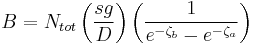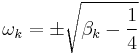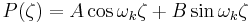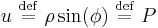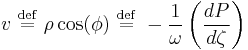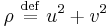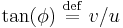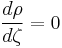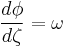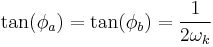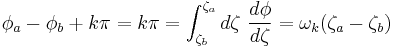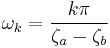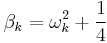Mason–Weaver equation
The Mason–Weaver equation (named after Max Mason and Warren Weaver) describes the sedimentation and diffusion of solutes under a uniform force, usually a gravitational field.[1] Assuming that the gravitational field is aligned in the z direction (Fig. 1), the Mason–Weaver equation may be written
where t is the time, c is the solute concentration (moles per unit length in the z-direction), and the parameters D, s, and g represent the solute diffusion constant, sedimentation coefficient and the (presumed constant) acceleration of gravity, respectively.
The Mason–Weaver equation is complemented by the boundary conditions
at the top and bottom of the cell, denoted as 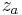 and
and 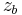 , respectively (Fig. 1). These boundary conditions correspond to the physical requirement that no solute pass through the top and bottom of the cell, i.e., that the flux there be zero. The cell is assumed to be rectangular and aligned with the Cartesian axes (Fig. 1), so that the net flux through the side walls is likewise zero. Hence, the total amount of solute in the cell
, respectively (Fig. 1). These boundary conditions correspond to the physical requirement that no solute pass through the top and bottom of the cell, i.e., that the flux there be zero. The cell is assumed to be rectangular and aligned with the Cartesian axes (Fig. 1), so that the net flux through the side walls is likewise zero. Hence, the total amount of solute in the cell
is conserved, i.e., 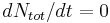 .
.
Contents |
Derivation of the Mason–Weaver equation
A typical particle of mass m moving with vertical velocity v is acted upon by three forces (Fig. 1): the drag force 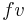 , the force of gravity
, the force of gravity 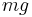 and the buoyant force
and the buoyant force 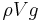 , where g is the acceleration of gravity, V is the solute particle volume and
, where g is the acceleration of gravity, V is the solute particle volume and  is the solvent density. At equilibrium (typically reached in roughly 10 ns for molecular solutes), the particle attains a terminal velocity
is the solvent density. At equilibrium (typically reached in roughly 10 ns for molecular solutes), the particle attains a terminal velocity  where the three forces are balanced. Since V equals the particle mass m times its partial specific volume
where the three forces are balanced. Since V equals the particle mass m times its partial specific volume 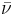 , the equilibrium condition may be written as
, the equilibrium condition may be written as
where 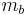 is the buoyant mass.
is the buoyant mass.
We define the Mason–Weaver sedimentation coefficient 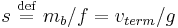 . Since the drag coefficient f is related to the diffusion constant D by the Einstein relation
. Since the drag coefficient f is related to the diffusion constant D by the Einstein relation
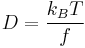 ,
,
the ratio of s and D equals
where 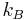 is the Boltzmann constant and T is the temperature in kelvins.
is the Boltzmann constant and T is the temperature in kelvins.
The flux J at any point is given by
The first term describes the flux due to diffusion down a concentration gradient, whereas the second term describes the convective flux due to the average velocity  of the particles. A positive net flux out of a small volume produces a negative change in the local concentration within that volume
of the particles. A positive net flux out of a small volume produces a negative change in the local concentration within that volume
Substituting the equation for the flux J produces the Mason–Weaver equation
The dimensionless Mason–Weaver equation
The parameters D, s and g determine a length scale 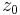
and a time scale 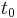
Defining the dimensionless variables 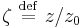 and
and 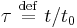 , the Mason–Weaver equation becomes
, the Mason–Weaver equation becomes
subject to the boundary conditions
at the top and bottom of the cell, 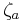 and
and 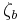 , respectively.
, respectively.
Solution of the Mason–Weaver equation
This equation may be solved by separation of variables. Defining 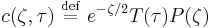 , we obtain the two equations coupled by a constant
, we obtain the two equations coupled by a constant 
where acceptable values of  are defined by the boundary conditions
are defined by the boundary conditions
at the upper and lower boundaries, 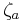 and
and 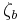 , respectively. Since the T equation has the solution
, respectively. Since the T equation has the solution 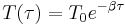 , where
, where 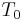 is a constant, the Mason–Weaver equation is reduced to solving for the function
is a constant, the Mason–Weaver equation is reduced to solving for the function 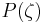 .
.
The ordinary differential equation for P and its boundary conditions satisfy the criteria for a Sturm–Liouville problem, from which several conclusions follow. First, there is a discrete set of orthonormal eigenfunctions 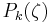 that satisfy the ordinary differential equation and boundary conditions. Second, the corresponding eigenvalues
that satisfy the ordinary differential equation and boundary conditions. Second, the corresponding eigenvalues 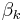 are real, bounded below by a lowest eigenvalue
are real, bounded below by a lowest eigenvalue 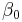 and grow asymptotically like
and grow asymptotically like 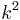 where the nonnegative integer k is the rank of the eigenvalue. (In our case, the lowest eigenvalue is zero, corresponding to the equilibrium solution.) Third, the eigenfunctions form a complete set; any solution for
where the nonnegative integer k is the rank of the eigenvalue. (In our case, the lowest eigenvalue is zero, corresponding to the equilibrium solution.) Third, the eigenfunctions form a complete set; any solution for 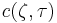 can be expressed as a weighted sum of the eigenfunctions
can be expressed as a weighted sum of the eigenfunctions
where 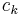 are constant coefficients determined from the initial distribution
are constant coefficients determined from the initial distribution 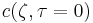
At equilibrium, 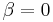 (by definition) and the equilibrium concentration distribution is
(by definition) and the equilibrium concentration distribution is
which agrees with the Boltzmann distribution. The 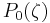 function satisfies the ordinary differential equation and boundary conditions at all values of
function satisfies the ordinary differential equation and boundary conditions at all values of 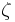 (as may be verified by substitution), and the constant B may be determined from the total amount of solute
(as may be verified by substitution), and the constant B may be determined from the total amount of solute
To find the non-equilibrium values of the eigenvalues 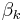 , we proceed as follows. The P equation has the form of a simple harmonic oscillator with solutions
, we proceed as follows. The P equation has the form of a simple harmonic oscillator with solutions 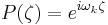 where
where
Depending on the value of 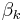 ,
, 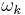 is either purely real (
is either purely real (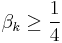 ) or purely imaginary (
) or purely imaginary (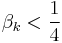 ). Only one purely imaginary solution can satisfy the boundary conditions, namely, the equilibrium solution. Hence, the non-equilibrium eigenfunctions can be written as
). Only one purely imaginary solution can satisfy the boundary conditions, namely, the equilibrium solution. Hence, the non-equilibrium eigenfunctions can be written as
where A and B are constants and  is real and strictly positive.
is real and strictly positive.
By introducing the oscillator amplitude  and phase
and phase  as new variables,
as new variables,
the second-order equation for P is factored into two simple first-order equations
Remarkably, the transformed boundary conditions are independent of  and the endpoints
and the endpoints 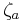 and
and 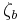
Therefore, we obtain an equation
giving an exact solution for the frequencies 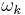
The eigenfrequencies 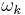 are positive as required, since
are positive as required, since 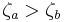 , and comprise the set of harmonics of the fundamental frequency
, and comprise the set of harmonics of the fundamental frequency 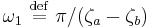 . Finally, the eigenvalues
. Finally, the eigenvalues 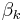 can be derived from
can be derived from 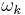
Taken together, the non-equilibrium components of the solution correspond to a Fourier series decomposition of the initial concentration distribution 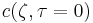 multiplied by the weighting function
multiplied by the weighting function 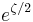 . Each Fourier component decays independently as
. Each Fourier component decays independently as 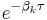 , where
, where 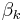 is given above in terms of the Fourier series frequencies
is given above in terms of the Fourier series frequencies 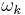 .
.
See also
References
- ^ Mason, M; Weaver W (1924). "The Settling of Small Particles in a Fluid". Physical Review 23: 412–426. Bibcode 1924PhRv...23..412M. doi:10.1103/PhysRev.23.412.
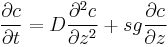
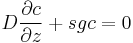
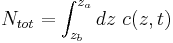
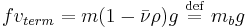
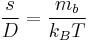
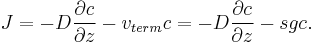
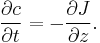
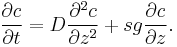
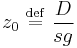
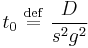
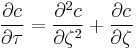
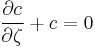
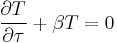
![\frac{\partial^{2} P}{\partial \zeta^{2}} %2B
\left[ \beta - \frac{1}{4} \right] P = 0](/2012-wikipedia_en_all_nopic_01_2012/I/7362c04dd9333370d3b69af7b4106b8c.png)